郑雨军教授课题组在量子系统演化速率极限统一理论研究工作中取得重要进展。他们建立发展了量子体系动力学演化速率极限的统一理论，所发展的量子速率极限统一理论既适用于厄米量子系统也适用于非厄米量子系统。相关研究成果以“Quantum Speed Limit Quantified by the Changing Rate of Phase” 为题，于2021年 8 月31日发表在物理类顶级期刊 Phys. Rev. Lett. （最新IF: 9.161）：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.100404

该论文第一作者为77779193永利集团博士后孙舒宁，通讯作者为郑雨军教授。

对量子体系中量子态演化的速率极限——量子体系从一个量子态演化到另外一个不同量子态的最短时间——的研究，对理解和认识量子物理的基本过程具有重要科学意义，同时，也对量子技术——量子态的快速反转、量子动力学过程的最优操控等具有实际意义。

量子体系的动力学演化由薛定谔方程给出，但薛定谔方程并不能直接确定量子体系动力学演化的速率极限。因此，人们发展了不同类型的量子速率极限：

1945年 Mandelstam 和 Tamm给出量子体系从一个量子态演化到与其正交量子态的最短时间与体系能量不确定度的关系—— Mandelstam-Tamm 界（MT bound）。1998年，Margolus 和Levitin建立了该时间与量子体系能量平均值的关系——Margolus-Levitin界（ML bound）。此后，人们把上述量子速率极限推广至开体系、多体量子体系等，并广泛研究了加速量子体系演化的物理内禀因素以及量子纠缠、量子相干、量子体系非马尔可夫性等对量子速率极限界的影响等。

郑雨军教授团队基于量子力学几何性质，应用希尔伯特空间动力学李群理论，建立发展了量子速率极限统一界：用量子体系相位变化率度量量子系统演化速率极限，同时，阐释了此前已有的不同类型量子速率极限界所蕴涵的物理含义：如果量子体系的动力学演化仅满足薛定谔方程，其动力学演化的量子速率极限由Mandelstam-Tamm 界给出；如果量子体系的动力学演化是满足薛定谔方程的（类）测地线演化，其动力学演化的量子速率极限由Margolus-Levitin界给出；如果量子体系的动力学演化是满足薛定谔方程的平行演化，其动力学演化的量子速率极限由该课题组在2019年所发展的极限界给出（参见： https://www.view.sdu.edu.cn/info/1021/125276.htm ）。

该研究建立了量子体系动力学演化速率极限与薛定谔方程的对应：量子体系的动力学演化由薛定谔方程给出，与此相应的量子速率极限则由动力学演化所积累相位的变化率确定。同时，该研究进一步扩展加深了人们对量子系统相位的理解和认识。

该工作得到国家自然科学基金、国家基础研究发展计划和77779193永利集团优秀博士研究生创新能力提升计划的资助。

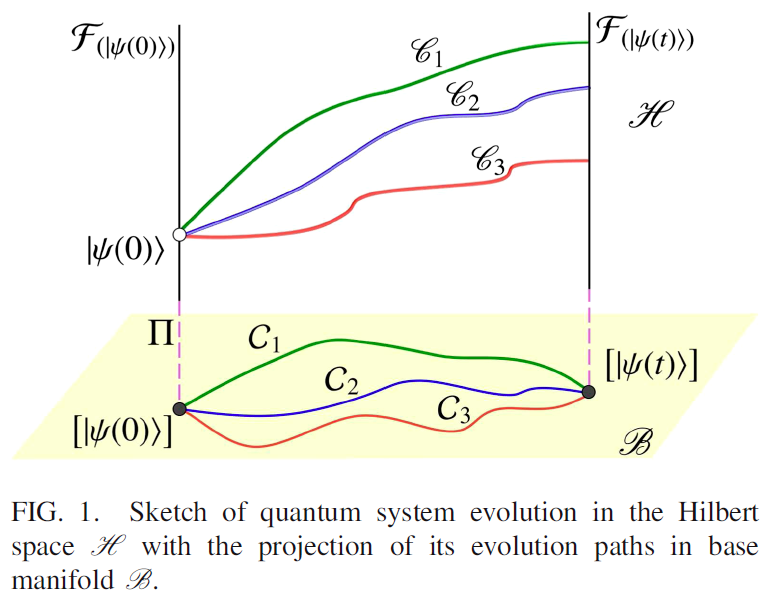
量子体系在希尔伯特空间H 中的演化及其在底流形B 中的投影示意图。

绿色曲线C ₁ 表示量子体系的动力学演化仅满足薛定谔方程，其动力学演化的量子速率极限由 Mandelstam-Tamm 界给出。蓝色曲线 C ₂ 表示量子体系的动力学演化是满足薛定谔方程的（类）测地线演化，其动力学演化的量子速率极限由 Margolus-Levitin 界给出。红色曲线 C ₃ 表示量子体系的动力学演化是满足薛定谔方程的平行演化，其动力学演化的量子速率极限由该课题组在 2019 年所发展的极限界给出。